Élaborez une carte mentale : nombre relatif pour maîtriser les concepts fondamentaux

Dans l’apprentissage des mathématiques, la maîtrise des nombres relatifs est un défi que rencontrent de nombreux élèves. Ces nombres, qu’ils soient positifs ou négatifs, possèdent des propriétés et des règles qui nécessitent une compréhension approfondie pour être manipulés efficacement. Dans cet article, nous allons explorer comment élaborer une carte mentale pour aider à visualiser et assimiler ces concepts fondamentaux liés aux nombres relatifs.

Comprendre les nombres relatifs : définition et importance

Pour débuter, il est essentiel de cerner ce que sont véritablement les nombres relatifs. Un nombre relatif est tout nombre qui peut être à la fois positif ou négatif, ainsi que le zéro. Cette dualité est cruciale en mathématiques, car elle permet de représenter des situations variées, allant des températures en dessous de zéro aux dettes financières.

Les nombres positifs sont généralement utilisés pour exprimer des valeurs supérieures à zéro, tandis que les nombres négatifs représentent des valeurs inférieures. Par exemple, une charge de +10 mètres pourrait signifier que l’on se situe au-dessus du niveau de la mer, alors qu’un déplacement de -5 mètres indiquerait une profondeur sous ce même niveau. Cette distinction entre les deux types de nombres est incontournable dans divers domaines scientifiques ainsi que dans la vie quotidienne.

Il est fortement recommandé d’utiliser des manuels scolaires ou des ressources éducatives tels que ceux de Manuel Scolaire Nathan, Hachette Éducation ou Belin Éducation pour approfondir cette compréhension des nombres relatifs. Ces ressources sont conçues pour offrir une approche pédagogique et structurée, facilitant ainsi l’assimilation de ces concepts.

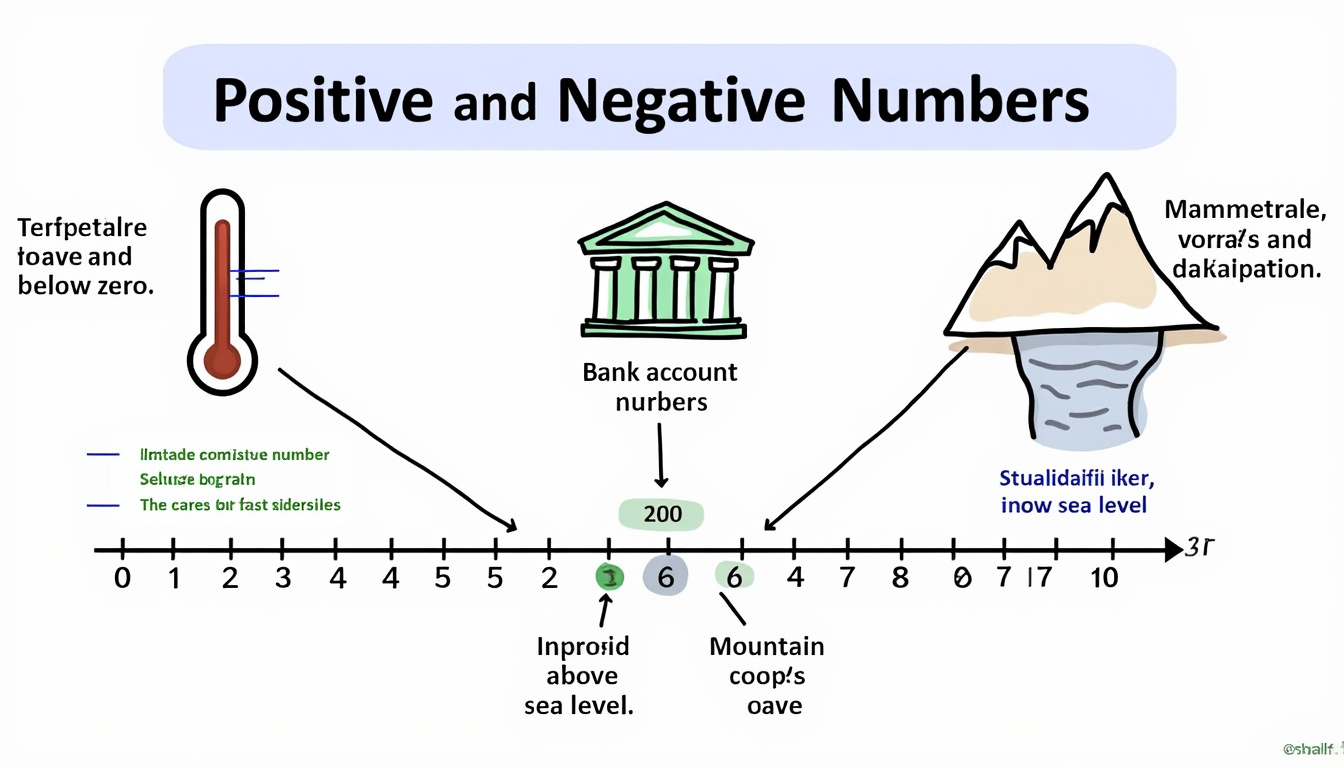
L’utilisation des nombres relatifs dans la vie quotidienne

Les applications des nombres relatifs se manifestent dans divers contextes, par exemple :

• Météorologie : Les températures peuvent descendre en dessous de zéro centigrade, notées alors comme des nombres négatifs.
• Finance : Les dettes sont généralement exprimées par des valeurs négatives dans les états financiers.
• Géographie : Les altitudes sont souvent représentes par des nombres positifs et négatifs, comme avec le niveau de la mer.

Ces exemples démontrent comment les nombres relatifs sont omniprésents dans notre vie quotidienne. En réalité, comprendre leur fonctionnement permet à quiconque d’être plus à l’aise avec ces concepts, notamment lors d’activités telles que la gestion des finances personnelles ou le suivi des prévisions météorologiques.

Les propriétés des nombres relatifs : addition et soustraction

Une fois familiarisés avec les nombres relatifs, il est primordial d’aborder les opérations qui leur sont associées, à savoir l’addition et la soustraction. Ces opérations suivent des règles spécifiques qui varient en fonction des signes des nombres manipulés. Voici un aperçu de ces règles :

Situation	Règle à appliquer
Deux nombres de même signe (ex : +3 et +5)	Additionner les valeurs et garder le signe (ex : +8)
Deux nombres de signes opposés (ex : +4 et -2)	Soustraire les valeurs et garder le signe du plus grand nombre (ex : +2)
Un nombre positif et un nombre négatif (ex : +7 et -3)	Soustraire les valeurs (7 – 3) et garder le signe du plus grand (ex : +4)
Deux nombres négatifs (ex : -4 et -6)	Ajouter les deux distances à zéro et conserver le signe négatif (ex : -10)

Ces règles sont essentielles pour effectuer des calculs précis avec des nombres relatifs. L’utilisation de cartes mentales peut s’avérer très bénéfique pour visualiser ces relations et règles afin de mieux les mémoriser. Des outils comme Mindomo permettent de créer ces cartes mentales, facilitant ainsi une révision efficace.

Conseils pour pratiquer l’addition et la soustraction des nombres relatifs

Pour mieux maîtriser ces opérations, voici quelques conseils pratiques :

1. Répéter les règles de manière régulière : la pratique rend parfait.
2. Utiliser des jeux et applications éducatives comme Les Bons Profs ou la Khan Academy en français pour rendre l’apprentissage interactif.
3. Travailler en groupe pour discuter et résoudre ensemble des problèmes complexes.
4. Consulter des ouvrages comme Bordas Mathématiques ou Éditions Magnard pour des exercices variés.

Ces stratégies peuvent grandement améliorer la compréhension des nombres relatifs. La clé réside dans la diversité des approches d’apprentissage et le désir d’approfondir chaque aspect des maths relatifs.

Multiplication et division des nombres relatifs : un défi supplémentaire

Passons maintenant aux opérations de multiplication et de division, qui introduisent un autre ensemble de règles. Lors de l’utilisation de nombres relatifs, les règles sont plutôt simples, mais il est essentiel de les comprendre pour éviter des erreurs fréquentes.

Voici les principes clés :

• Produits de signes : Le produit de deux nombres de même signe (par exemple, +4 x +3) est positif, tandis que le produit de deux nombres de signes opposés (par exemple, +4 x -3) est négatif.
• Quotients de signes : De même, le quotient de deux nombres de même signe est positif, et le quotient de signes opposés est négatif.

Situation	Règle à appliquer
Deux nombres positifs (ex : +2 et +3)	Résultat positif (ex : 6)
Deux nombres négatifs (ex : -2 et -3)	Résultat positif (ex : 6)
Un nombre positif et un nombre négatif (ex : +2 et -3)	Résultat négatif (ex : -6)
Un nombre négatif et un nombre positif (ex : -2 et +3)	Résultat négatif (ex : -6)

Ces opérations illustrent encore une fois la nécessité d’une bonne compréhension des concepts fondamentaux des nombres relatifs. Pour mieux appréhender ces concepts, de nombreuses ressources en ligne, telles que Mathenpoche et Le Livre Scolaire, fournissent des explications pratiques et des exercices.

Comment pratiquer la multiplication et la division des nombres relatifs efficacement

Pour maîtriser les multiplications et les divisions, voici quelques suggestions :

1. Créer des fiches de révision pour chaque règle.
2. Utiliser des jeux d’application de mathématiques pour des entraînements ludiques.
3. Discuter et expliquer les concepts à un pair pour renforcer votre compréhension.
4. Utiliser des vidéos explicatives disponibles sur des plateformes comme YouTube pour visualiser les concepts.

Ces pratiques vous aideront à solidifier votre maîtrise sur ce sujet complexe mais fascinant des nombres relatifs.

Les nombres opposés et leur principe de symétrie

Un autre concept important à maîtriser en ce qui concerne les nombres relatifs est celui des nombres opposés. Deux nombres sont dits opposés lorsqu’ils possèdent la même distance à zéro sur la droite numérique mais des signes différents. Par exemple, +5 et -5 sont des opposés.

Ce principe de symétrie est essentiel non seulement en mathématiques, mais aussi dans de nombreux domaines. Par exemple, les concepts de gain et de perte, de succès et d’échec, peuvent trouver leur inspiration dans cette notion. En mathématiques, la notion d’opposés est fondamentalement corrélée à l’addition et à la soustraction : l’addition de deux opposés donnerait toujours zéro.

Exemples d’application du concept d’opposés

Voici quelques contextes dans lesquels les nombres opposés jouent un rôle crucial :

• Économie : Un profit peut être considéré comme un nombre positif, alors qu’une perte peut être vue comme son opposé.
• Géométrie : Lors de la réflexion d’une figure géométrique autour de l’origine d’un plan cartésien.
• Sciences : Dans des études thermodynamiques, la chaleur et le froid peuvent être considérés comme des valeurs opposées.

Comprendre les nombres opposés aide à appréhender les situations où la balance est importante, ce qui est une compétence vitale dans diverses carrières professionnelles et quotidiennes.

Irregard des nombres relatifs dans le monde numérique : applications avancées

Dans le monde numérique d’aujourd’hui, la compréhension des nombres relatifs prend une nouvelle dimension. Que ce soit dans le codage, le design graphique ou l’évaluation de systèmes financiers, ces nombres sont omniprésents. Les algorithmes modernes utilisent souvent des bogues relatifs pour représenter des différences de valeurs et les ajustements nécessaires dans divers contextes.

Les implications en matière de technologie sont nombreuses. Prenons l’exemple du développement d’algorithmes de recherche. Ces derniers doivent souvent gérer des données positives et négatives lors d’analyses de résultats, ce qui implique une solide maîtrise des nombres relatifs. Cela inclut les ajustements pour chaque résultat, prenant en compte les variations.

Importance de la maîtrise des nombres relatifs pour les carrières numériques

Pour ceux qui envisagent une carrière dans le domaine de l’informatique ou des données, la compréhension des nombres relatifs est fondamentale. Les entreprises cherchent des candidats capables d’utiliser ces concepts dans des applications pratiques. Voici comment :

• Analyse de données : Au sein d’une entreprise, les analystes utilisent fréquemment des nombres relatifs pour interpréter des mélanges de données.
• Développement de logiciels : Les développeurs doivent comprendre ces concepts lorsqu’ils traitent des erreurs et des codes.
• Statistiques : Les statisticiens appliquent souvent des modèles basés sur des nombres relatifs pour des prévisions et des rapports.

Ces applications montrent clairement que la maîtrise des nombres relatifs n’est pas seulement une compétence mathématique, mais également une compétence essentielle pour naviguer dans le monde numérique de 2025 et au-delà.

Pratiques de révision et ressources éducatives

Pour conclure notre exploration, il est essentiel d’aborder les différentes stratégies de révision et les ressources disponibles pour renforcer la compréhension des nombres relatifs. Il existe de nombreuses plateformes qui peuvent aider les élèves à pratiquer ces concepts à travers des exercices interactifs et des tutoriels.

Voici quelques ressources utiles :

• Mathenpoche – Une plateforme d’exercices en ligne.
• Le Livre Scolaire – Propose des manuels digitaux et des exercices.
• Khan Academy en français – Formations gratuites sur divers concepts mathématiques.
• Les Bons Profs – Offre des vidéos explicatives et des supports de révisions.

Prendre le temps d’explorer ces plateformes peut significativement améliorer vos compétences en mathématiques et renforcer votre compréhension des nombres relatifs, ce qui vous préparera au succès dans ce domaine.

Ressources supplémentaires pour approfondir vos connaissances

En plus des plateformes mentionnées, voici d’autres instructions et exercices recommandés :

1. Accéder aux ressources de Hatier Mathématiques pour des exercices de niveau adapté.
2. Explorer Bordas Mathématiques pour des révisions spécifiques aux nombres relatifs.
3. Utiliser les tutoriels sur Éditions Magnard pour des concepts mathématiques avancés.
4. Visionner les simulations pédagogiques sur La Khan Academy en français.

Ces ressources, en plus d’être disponibles en ligne, offrent diverses approches d’apprentissage adaptées à tous les niveaux et styles éducatifs, stimulant ainsi l’apprenant à explorer le monde fascinant des nombres relatifs.

Questions fréquentes

Qu’est-ce qu’un nombre relatif ?

Un nombre relatif est un nombre qui peut être positif ou négatif, incluant le zéro.

Comment additionner des nombres relatifs de signes différents ?

Il faut soustraire leur valeur et garder le signe du nombre avec la plus grande valeur.

Comment savoir si un produit de deux nombres relatifs est positif ou négatif ?

Si les deux nombres ont le même signe, le résultat est positif ; s’ils ont des signes opposés, le résultat est négatif.

Où puis-je trouver des exercices sur les nombres relatifs ?

Des plateformes telles que Mathenpoche et Khan Academy en français offrent de nombreux exercices interactifs.

Quelles sont les applications pratiques des nombres relatifs ?

Les nombres relatifs sont utilisés en finance, en météorologie, en géographie, et dans bien d’autres domaines.